Skip to content

monkeynut.org

Tic Tac Toe in TLA+

Although I've written many informal specifications of software as part of my employments, I haven't ever written any formal specifications (and for good reason: in most domains, the return-on-investment likely isn't there). I like to pretend to myself that given enough time, I probably could write a formal specification, but what's it like to actually do this?

Here I go through the exercise of writing a formal specification of Tic Tac Toe in TLA+ / PlusCal, and then use the associated TLC model checker to see whether an example game is winnable. This felt like just the right level of difficulty to get a feel for writing a formal specification, and had the nice payoff of actually being "useful" for something!

(Below I give code highlights; for the full details see here.)

The game state

We need to start by defining our game state, which involves a couple of TLA+ definitions.

First we need to know what the current board state is. For this, we're going to use a matrix, where the string "atoms" have the obvious meanings:

board = <<
   <<"o", ".", "x">>,
   <<".", "o", ".">>,
   <<".", ".", ".">> 
>>;

Secondly, we need to know which player is next to go:

player = "x";

Supporting TLA+ definitions

With the game state defined, we next define a TLA+ formula for what is means for a player p to win. Here \E and \A are the existential and universal quantifiers.

winner(p) ==
  (* Rows *)
  \/ \E i \in 1..3: \A j \in 1..3: board[i][j] = p
  (* Columns *)
  \/ \E j \in 1..3: \A i \in 1..3: board[i][j] = p
  (* Diagonals *)
  \/ \A i \in 1..3: board[i][i] = p
  \/ \A i \in 1..3: board[4-i][i] = p

We also need to define what it means for there to be an unfilled board space:

unfilled == \E i \in 1..3: \E j \in 1..3: board[i][j] = "."

The game algorithm

Finally, we define our game algorithm in PlusCal, which will be automatically translated into TLA+. Note the use of with for non-deterministic choice (the model checker will explore all possible instantiations for us).

while unfilled /\ ~(winner("o") \/ winner("x")) do
  with i \in 1..3, j \in 1..3 do
    if board[i][j] = "." then
      board[i][j] := player;
      if player = "x" then player := "o" else player := "x" end if;
    end if;
  end with;
end while;
assert ~winner("x");

Using the TLC model checker

When we run this from the model checker, we see that it's possible to reach a state where where our "x isn't the winner" assertion fails:

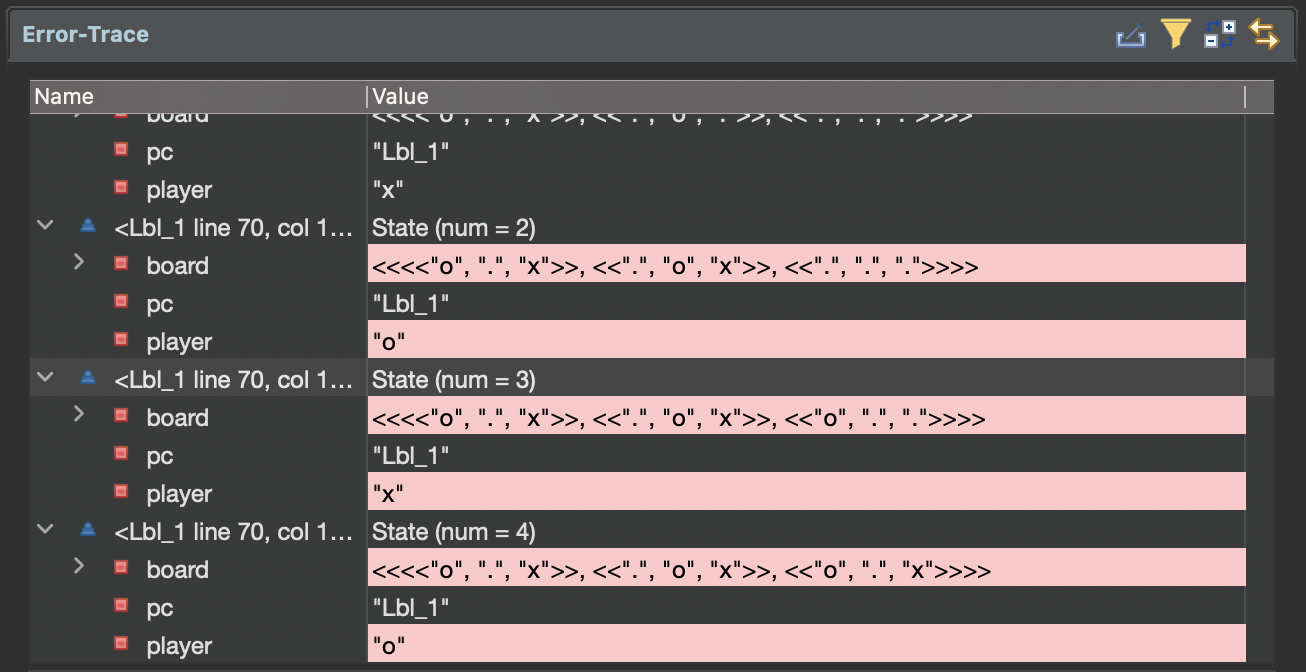
image description

Good luck x!

Takeaways

(Caveats: I am not an expert, these are my takeaways, this was just a toy example etc.)

I was initially wary of writing the definitions in "math", but it actually ended up feeling liberating not having to define implementation details! For example, I loved that I could write existential and universal quantifiers, know that the model checker would automatically handle the "implementation" of them.

With that said, I liked that I could still write the game algorithm in PlusCal (making use of TLA+ definitions); this gave the game algorithm a familiar, imperative feel. Which is exactly the point of PlusCal! It was also useful from the point-of-view of learning TLA+ to hit Command+T and see the corresponding TLA+ next-state relation.

I can imagine eventually writing everything in TLA+, but for now I'll probably stick with a hybrid TLA+ / PlusCal approach.

Resources

2 June 2023